최대 힙에서의 삭제 연산은 제일 큰 값인 루트 노드 삭제 연산만 존재한다. 방법은 다음과 같다.
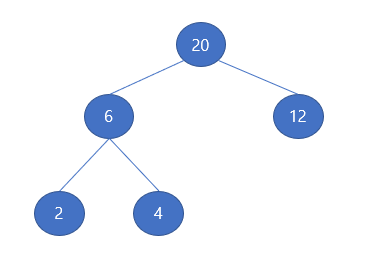
위와 같은 트리가 있을 때 루트 노드 20을 삭제한다고 가정하면
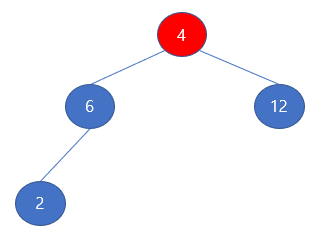
트리의 가장 마지막 노드인 4를 루트 노드와 맞바꾼다.

4의 자식 노드인 6과 12를 비교했을 때 더 큰 값을 가지는 쪽과 맞바꾼다. 그럼 최대힙의 성질을 만족 할 수 있다.
이러한 삭제 연산 또한 삽입 연산의 시간복잡도와 같은 O(logn)이다. 이를 구현한 코드는 다음과 같다.
class MaxHeap:
def __init__(self):
self.data = [None]
def remove(self):
if len(self.data) > 1:
self.data[1], self.data[-1] = self.data[-1], self.data[1]
data = self.data.pop(-1)
self.maxHeapify(1)
else:
data = None
return data
def maxHeapify(self, i):
# 왼쪽 자식 (left child) 의 인덱스를 계산합니다.
left = 2*i
# 오른쪽 자식 (right child) 의 인덱스를 계산합니다.
right = 2*i+1
smallest = i
# 왼쪽 자식이 존재하는지, 그리고 왼쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
if left < len(self.data) and self.data[left] > self.data[smallest] :
# 조건이 만족하는 경우, smallest 는 왼쪽 자식의 인덱스를 가집니다.
smallest=left
# 오른쪽 자식이 존재하는지, 그리고 오른쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
if right< len(self.data) and self.data[right] > self.data[smallest] :
# 조건이 만족하는 경우, smallest 는 오른쪽 자식의 인덱스를 가집니다.
smallest=right
if smallest != i:
# 현재 노드 (인덱스 i) 와 최댓값 노드 (왼쪽 아니면 오른쪽 자식) 를 교체합니다.
self.data[i],self.data[smallest]=self.data[smallest],self.data[i]
# 재귀적 호출을 이용하여 최대 힙의 성질을 만족할 때까지 트리를 정리합니다.
self.maxHeapify(smallest)
'기초 알고리즘' 카테고리의 다른 글
| 파이썬) 최대 힙(Heap) (0) | 2023.02.07 |
|---|---|
| 파이썬) 이진 탐색 트리 삭제 연산 (0) | 2023.02.06 |
| 파이썬) 이진 탐색 트리 (0) | 2023.02.04 |
| 파이썬) 이진 트리 넓이 우선 순회 연산 (0) | 2023.02.03 |
| 파이썬) 이진 트리 깊이 우선 순회 연산 (0) | 2023.02.02 |