이진 탐색 트리란 모든 노드에 대해서(중복되는 데이터 원소는 없는 것으로 가정)
- 왼쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 작고
- 오른쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 큰
두 성질을 만족하는 이진 트리이다.
이진 트리의 예시로 다음과 같이 들 수 있다.

루트 노드 5를 기준으로 했을 때 왼쪽 서브트리는 모두 5보다 작고, 오른쪽 서브트리는 모두 5보다 크다.
이러한 성질 덕분에 트리안에 특정 원소를 찾는 과정이 매우 쉬워진다.
만약 6을 찾는다고 가정하면 6은 루트노드 5보다 크므로 오른쪽으로, 그 다음 8보다 작으므로 왼쪽으로 가기만 하면 된다.
배열을 이용한 이진 탐색과 비슷한 원리를 가지고 있다.

이진 탐색 트리의 탐색 과정 또한 시간 복잡도가 O(logn)이 된다.
탐색외의 이진 탐색 트리의 연산들을 정리하면 다음과 같다.
- insert(key, data) : 트리에 주어진 데이터 원소를 추가
- remove(key) : 특정 원소를 트리로부터 삭제
- lookup(key): 특정 원소를 검색
- inorder(): 키의 순서대로 데이터 원소 나열
- min(), max() : 최소 키, 최대 키를 가지는 원소를 각각 탐색
insert를 제외한 나머지 연산은 트리에 새 노드가 따로 추가되는 연산은 아니다. 그렇다면 삽입 연산이 실행되면 이진 탐색 트리는 어떠한 과정이 일어나는지 살펴보자면
ex) 3을 삽입하는 경우
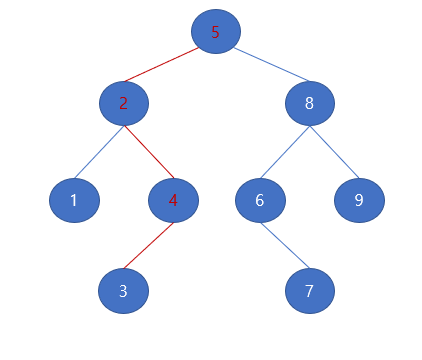
먼저 루트 노드 5와 3을 비교하면 3이 더 작으므로 왼쪽으로 간다. 다음 2보다 크므로 오른쪽, 다음 4보다 작으므로 왼쪽으로 간다. 4의 왼쪽 자리는 기존에 빈 자리이므로 3을 삽입한다.
이진 탐색 트리를 구현하기 위한 코드는 다음과 같다.
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.left = None
self.right = None
class BinSearchTree:
def __init__(self):
self.root = None
이진 탐색 트리의 inorder() 연산 코드는 다음과 같다.
class Node:
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self)
if self.right:
traversal += self.right.inorder()
return traversal
class BinSearchTree:
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []이진 트리의 중위 순회 연산 코드와 같이 재귀적으로 구현할 수 있다.
최대,최소 값을 찾는 코드는 다음과 같다.
class Node:
def min(self):
if self.left:
return self.left.min()
else:
return self
def max(self):
if self.right:
return self.right.max()
else:
return self이진 탐색 트리의 특성상 최솟값을 찾으려면 트리의 왼쪽 맨 아래로, 최대값을 찾으려면 오른쪽 아래로 계속 내려가면 저절로 구해진다.
삽입 연산의 코드는 다음과 같다.
class Node:
def insert(self, key, data):
if key<self.key: # 삽입 원소가 루트(또는 그 이후)노드보다 작다면
if self.left:
self.left.insert(key, data)
else:
self.left = Node(key, data)
elif key>self.key: # 삽입 원소가 루트(또는 그 이후)노드보다 크다면
if self.right:
self.right.insert(key, data)
else:
self.right = Node(key, data)
else:
raise KeyError('...')
class BinSearchTree:
def insert(self, key, data):
if self.root:
self.root.insert(key, data)
else: # 빈 트리라면
self.root = Node(key, data)맨 처음 루트노드와 삽입할 원소를 비교한다면, 대소관계에 따라 왼쪽 또는 오른쪽으로 이동할 것이고, 만약 자식 노드가 없다면 크기에 맞는 위치에 key값을 가진 노드를 최종 삽입하는 재귀적인 방법이다.
'기초 알고리즘' 카테고리의 다른 글
| 파이썬) 최대 힙(Heap) (0) | 2023.02.07 |
|---|---|
| 파이썬) 이진 탐색 트리 삭제 연산 (0) | 2023.02.06 |
| 파이썬) 이진 트리 넓이 우선 순회 연산 (0) | 2023.02.03 |
| 파이썬) 이진 트리 깊이 우선 순회 연산 (0) | 2023.02.02 |
| 파이썬) 트리(Tree) (0) | 2023.02.01 |