중위 표기법은 우리가 일상에 쓰는 수식 표기법으로 연산자의 두개의 피연산자 사이에 있는 표기법을 말한다.
ex) A*B+C
후위 표기법은 연산자를 두개의 피연산자 뒤에 표기하는 기법이다.
ex) A*B+C -> A B * C +
위 중위 표기법이 어떤 과정을 통해 후위 표기법으로 바뀌는 지 그림으로 표현하면
A*B+C
1.
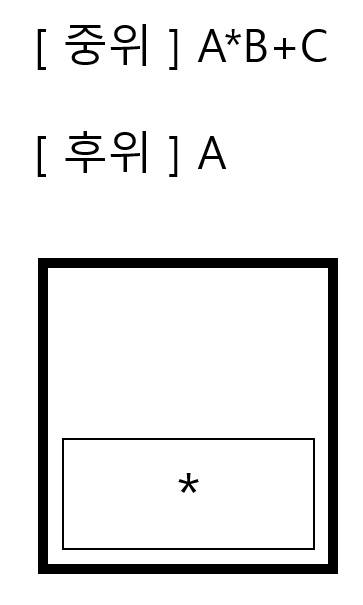
후위 표기식을 담을 빈 리스트가 있고, 연산자를 넣을 스택이 있다고 가정하자. 중위 표기식의 왼쪽부터 차례대로 읽어나가는데 피연산자인 경우 후위 표기식 리스트에 넣는다. 그 다음 연산자 *는 빈 스택에 push한다.
2.
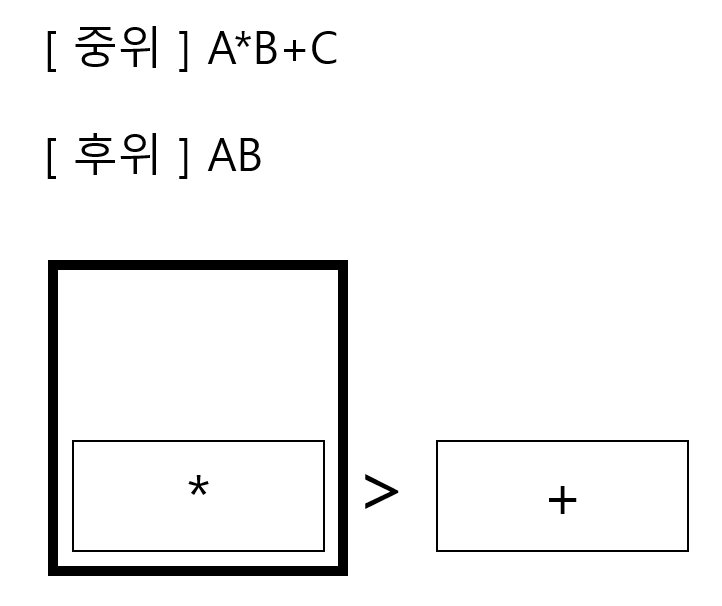
B는 피연산자이기 때문에 후위 표기식 리스트에 넣고, +를 스택에 push하기전 연산자의 우선순위를 비교한다. *는 +보다 연산의 우선순위이기 때문에 우선 *를 스택에서 빼고 후위 표기식 리스트에 넣는다. 그 다음 +를 스택에 push한다.
3.

피연산자 C를 리스트에 넣고나면 중위 표기식을 다 읽어들이게 된다. 그 후에는 스택에 남아있는 연산자를 pop을 이용해 빼낸 후 리스트에 넣는다. 그렇다면 최종 결과는 A B * C +가 된다.
A+B*C
위 경우는 연산자의 우선순위가 위의 예시와 뒤바뀐 경우이다.

A, +, B까지 읽어들인 후 연산자 *를 읽을 차례를 보면 +는 *보다 연산 우선순위가 낫다. 따라서 +가 이미 push되어 있는 스택에 *를 push한다. 그 다음 C를 리스트에 추가하면 스택에는 위와 같이 *,+가 남는다. 이를 pop()을 한 후 리스트에 추가한다. 따라서 최결과는 ABC*+가 된다.
괄호가 있는 경우 (A+B)*C
1.

괄호같은 경우도 스택에 넣는데 괄호의 연산 우선순위를 최하위라 가정한다. 따라서 +는 ( 위에 push된다.
2.

닫는 괄호 )를 읽게되면 스택에서 ( 가 나올때까지 pop을 한다. ( 이전에 연산자가 있다면 그 연산자는 후위 표기식 리스트에 추가한다. 그 후 괄호는 버린다.
3.

피연산자 C를 읽고 난후 *는 스택에 추가된다. 그 후 스택에 남은 연산자를 리스트 뒤에 붙인다. 따라서 최종 결과는 AB+C* 가 된다.
규칙을 총 정리하면 다음과 같다.
중위 표현식을 왼쪽부터 한 글자씩 읽어서
- 피연산자이면 그냥 출력
- ( 이면 스택에 push
- ) 이면 (이 나올때까지 스택에서 pop, 출력
- 연산자이면 스택에서 이보다 높거나 같은 우선순위 것들을 pop,출력 그리고 이 연산자는 스택에 push
다 읽고 난 후 스택에 남아 있는 연산자를 모두 pop, 출력한다.
이를 코드로 구현하면 다음과 같다.
prec = {
'*': 3, '/': 3,
'+': 2, '-': 2,
'(': 1
} # 연산자 우선순위 설정
def solution(S):
opStack = ArrayStack()
answer = ''
for s in S:
if s not in '+-*/()': # 피연산자인 경우 그냥 answer에 추가
answer+=s
elif s == '(': # ( 이면 스택에 push
opStack.push(s)
elif s == ')': # ) 이면 (가 나올 때까지 스택을 pop한 후 answer에 추가
while not opStack.isEmpty():
a = opStack.pop()
if a == '(':
break
else:
answer += a
else: # 연산자인 경우
if opStack.isEmpty(): # 스택이 비어있으면 스택에 push
opStack.push(s)
elif not opStack.isEmpty(): # 스택이 비어있지 않다면 우선순위 비교
while not opStack.isEmpty():
if prec[opStack.peek()] >= prec[s]:
answer += opStack.pop()
else:
break
opStack.push(s)
while not opStack.isEmpty(): # 스택에 남아 있는 연산자 모두 answer에 추가
answer += opStack.pop()
return answer
위 코드는 필자가 작성한 것이기 때문에 효율적인 답이 아닐 수 있습니다
'기초 알고리즘' 카테고리의 다른 글
| 파이썬) 큐(Queues) (0) | 2023.01.29 |
|---|---|
| 파이썬) 후위 표기법 수식을 계산하기 (1) | 2023.01.28 |
| 파이썬) 스택(Stack) (0) | 2023.01.25 |
| 파이썬) 양방향 연결 리스트 연산 (0) | 2023.01.24 |
| 파이썬) 더미 노드가 있는 연결 리스트 연산 (0) | 2023.01.23 |