데이터 원소들을 순서를 지어 늘어놓는다는 점에서 연결 리스트 (linked list) 는 선형 배열 (linear array) 과 비슷한 면이 있지만, 선형 배열은 "번호가 붙여진 칸에 원소들을 채워넣는" 방식이라고 한다면, 연결 리스트는 "각 원소들을 줄줄이 엮어서" 관리하는 방식에 차이점이 있다.
기본적 연결 리스트

위 그림과 같이 단순히 데이터가 늘어져있는 것이 아닌 앞에 있는 원소가 그 다음 원소를 가리키는 형식의 리스트를 연결 리스트라고 한다.
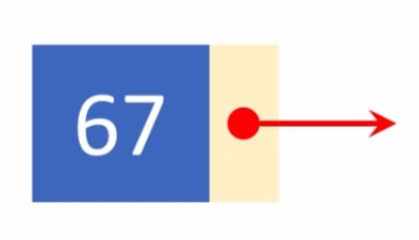
하나의 원소와 그 다음 원소를 가리키는 방향이 하나씩 담겨있는 것을 노드(Node)라고 한다. 위 노드에서 67은 노드의 data, 화살표는 link를 의미 한다. 노드내의 데이터는 숫자뿐만 아니라 문자열, 또 다른 연결리스트 등이 올 수 있다.
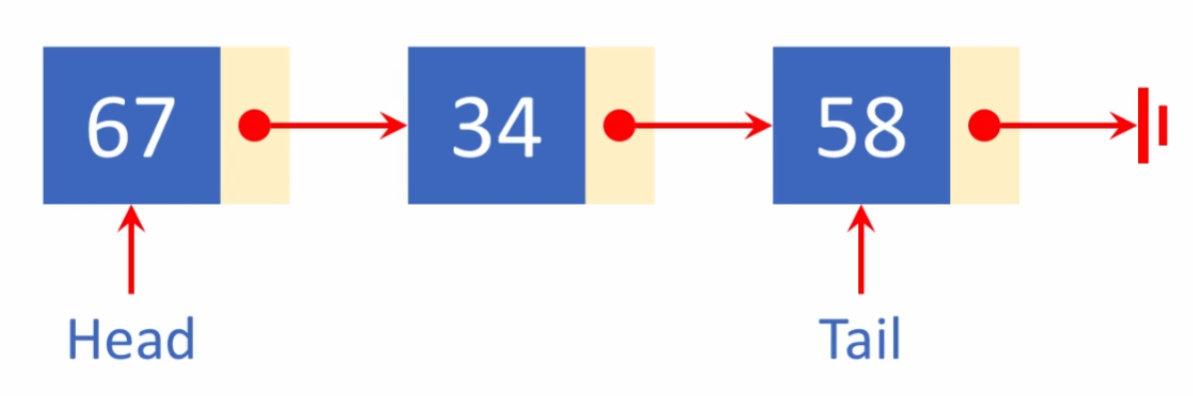
위 연결리스트에서 67이 담긴 노드는 첫 시작 노드인 Head, 58이 담긴 노드는 마지막 노드인 Tail이다.
위 연결 리스트와 노드를 코드로 구현하기 위한 방법은 아래와 같다.

우선 위와 같이 처음 노드를 만들기 위한 코드는 다음과 같다.
class Node:
def __init__(self,item):
self.data=item
self.next=None클래스를 처음 노드를 생성할때의 코드이다. 생성자의 인자로 주어진 item을 self.data에 담고, 노드가 처음 생성됐을 땐 연결된 다음 노드는 없으므로 self.next는 None으로 구성한다.
다음으로 비어 있는 연결리스트를 만들기 위한 코드는 다음과 같다.
class Linkedlist:
def __init__(self):
self.nodeCount=0
self.head=None
self.tail=NonenodeCount는 노드의 개수를 의미하는데 비어 있는 연결리스트를 만들기 때문에 그 개수는 0이다. 노드의 head와 tail 또한 존재하지 않기 때문에 그 값은 None이다.
위 두 클래스에 어떤 연산을 적용해 연결 리스트의 속성을 프로그래밍 할 수 있다.
* 연결 리스트의 특정 원소 참조하기
연결 리스트에서 특정 원소를 참조하 방법은 head부터 시작해 모든 노드를 비교하는 알고리즘이다.
def getAt(self, pos):
if pos < 1 or pos > self.nodeCount:
return None
i = 1
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr정의는 위와 같이 할 수 있다. 여기서 pos는 찾고자 하는 원소를 가진 노드의 위치이다. 어떤 연결리스트가 있을 때 노드의 개수를 나타내는 self.Count의 값이 0이면 빈 연결 리스트이고, pos값이 self.Count보다 크다면 즉 마지막 노드의 위치보다 더 큰 위치에 있다면 찾고자하는 원소 pos는 없으므로 None을 return한다.
그 외의 경우에는 위에서 언급했듯이 리스트의 head부터 비교해 나간다.
i=1부터 시작해 pos보다 작을 동안만 self.head의 다음 노드로 넘어가고, 같아질 경우 참조할 노드를 return하게 된다.
연결 리스트에서 특ㄹ정 원소를 참조할 때의 시간 복잡도는 O(n)이 된다.
* 리스트 내 모든 노드 출력하기
임의의 리스트 L에 들어 있는 노드들이 43 -> 85 -> 62 라면 [43, 85, 62]를 출력하고, 빈 리스트는 []를 출력하는 코드를 필자는 다음과 같이 구성하였다.
def traverse(self):
answer = []
curr = self.head
if curr==None:
return answer
while curr !=None:
answer.append(curr.data)
curr = curr.next
return answer노드의 head를 현재 위치라는 뜻의 curr로 명시하였고, curr이 None이면 빈 리스트이기 때문에 빈 리스트를 return하도록 했고 그렇지 않은 경우는 curr이 None이 될때까지, 즉 tail까지 읽고 다음 노드 None이 되기전까지 빈 리스트에 해당하는 노드를 append하고 다음 노드로 넘어가도록 구성하였다.
* 연결 리스트 내의 원소 삽입

위 그림과 같이 newNode를 리스트의 특정 위치에 삽입하는 것을 코드로 구성하면 다음과 같다.
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos == 1:
newNode.next = self.head
self.head = newNode
else:
if pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
newNode.next = prev.next
prev.next = newNode
if pos == self.nodeCount + 1:
self.tail = newNode
self.nodeCount += 1
return True
pos가 노드내에 없는 경우
if pos < 1 or pos > self.nodeCount + 1:
return Falsepos가 head이전이나 tail 다음 칸으로 지정되면 삽입을 할 수 없기 때문에 False를 return한다.
head앞에 삽입하려는 경우
if pos == 1:
newNode.next = self.head
self.head = newNode삽입하려는 newnode의 다음 노드는 기존 노드의 head가 될 것이고, 기존 노드의 head는 삽입되는 newNode가 head가 될것이므로 위와 같이 코드를 구성할 수 있다.
tail뒤에 삽입하려는 경우
else:
if pos == self.nodeCount + 1:
prev = self.tail
newNode.next = prev.next
prev.next = newNodetail뒤에 삽입하게 되면 기존 노드의 tail은 이전값 prev로 지정되고, 삽입될 newNode의 다음 노드는 기존 tail의 다음 노드와 같게된다. 그리고 기존 tail의 다음 노드는 삽입될 newNode가 되기 때문에 위와 같이 코드를 구성할 수 있다.
중간에 삽입하려는 경우
else:
prev = self.getAt(pos - 1)
newNode.next = prev.next
prev.next = newNode
삽입하려는 노드 위치 이전 노드를 prev로 명시한다. 이를 앞서 구성했던 특정 원소를 참조하는 코드 getAt(pos-1)을 이용한다. 그렇게 되면 삽입될 newNode의 다음 노드는 prev의 다음 노드와 같게된다. 그리고 prev의 다음 노드는 삽입될 newNode가 되기 때문에 위와 같이 코드를 구성할 수 있다.
위 네 경우를 실행한 뒤에 노드가 하나 삽입되므로 self.Count에 1을 더해주었다.
연결 리스트에 원소를 삽입할때 시간 복잡도는 다음과 같다.
- 맨 앞에 삽입하는 경우 : O(1)
- 중간에 삽입하는 경우 : O(n)
- 맨 끝에 삽입하는 경우 : O(1)
* 연결 리스트 내의 원소 삭제

pos가 가리키는 위치의 노드를 삭제하고 그 노드를 리턴하는 코드를 필자는 다음과 같이 구성했다.
def popAt(self, pos):
answer=self.getAt(pos)
if pos < 1 or pos > self.nodeCount:
raise IndexError
if pos == 1:
if self.nodeCount == 1:
self.head=None
self.tail=None
self.nodeCount = 0
else:
self.head = self.head.next
self.nodeCount -= 1
return answer.data
else:
prev = self.getAt(pos - 1)
prev.next = answer.next
if pos == self.nodeCount:
prev.next = None
self.tail = prev
self.nodeCount -= 1
return answer.data우선 삭제할 노드를 return해야 하므로 원소 참조 getAt을 이용해 answer로 명시하였다.
삭제할 원소가 노드 영역 바깥에 있는 경우
if pos < 1 or pos > self.nodeCount:
raise IndexError위 코드는 삭제할 원소가 노드 영역 바깥에 있는 경우에 IndexError exception 을 발생시키도록 하는 코드이다.
삭제할 원소가 head인 경우
if pos == 1:
if self.nodeCount == 1:
self.head=None
self.tail=None
self.nodeCount = 0
else:
self.head = self.head.next
self.nodeCount -= 1이 경우 또 두 경우로 나뉘게 된다. 첫번째는 주어진 리스트의 노드 개수가 1개밖에 없는 경우이다. 그 경우 노드를 삭제하면 빈 리스트가 되므로 Linkedlist 클래스 부분을 이용하였다.
그렇지 않은 경우 기존 노드의 head가 삭제되면 다음 노드가 head가 되고, 노드의 개수는 하나가 줄어드므로 위와 같이 코드를 구성했다.
삭제할 원소가 중간에 있는 경우
else:
prev = self.getAt(pos - 1)
prev.next = answer.next삭제할 위치 이전 위치의 노드를 고 특정 원소 참소 코드 getAt(pos-1)을 이용해 prev로 명시하였다. pos위치의 원소를 삭제하게되면 prev의 다음 노드는 삭제될 원소의 다음 노드와 같게된다.
삭제할 원소가 마지막에 있는 경우
if pos == self.nodeCount:
prev.next = None
self.tail = prev이 경우 pos 이전 노드가 tail이 되므로 prev의 다음 노드는 None이고, 기존 노드의 tail은 prev가 되므로 위와 같이 구성할 수 있다.
위 네 경우를 실행하게되면 노드가 하나 줄어드므로 self.Count에 1을 빼주었다.
연결 리스트에 원소를 삭제할때 시간 복잡도는 다음과 같다.
- 맨 앞에서 삭제하는 경우 : O(1)
- 중간에서 삭제하는 경우 : O(n)
- 맨 끝에서 삭제하는 경우 : O(n)
'기초 알고리즘' 카테고리의 다른 글
| 파이썬) 양방향 연결 리스트 연산 (0) | 2023.01.24 |
|---|---|
| 파이썬) 더미 노드가 있는 연결 리스트 연산 (0) | 2023.01.23 |
| 파이썬) 알고리즘의 복잡도와 Big-O 표기법 (0) | 2023.01.19 |
| 파이썬) 재귀 알고리즘 (0) | 2023.01.18 |
| 파이썬) 정렬(sort)과 탐색(search) (0) | 2023.01.17 |